Los polígonos

Un polígono es la figura geométrica de un plano que está establecida por líneas rectas. Se trata de un fragmento plano que está formado por segmentos consecutivos sin alineación, que reciben el nombre de lados.

Ahora ya que sabemos que son, enfoquémonos en su clasificación.

Por sus lados

Los polígonos se pueden clasificar según su número de lados: 

• Triángulo: polígono con tres lados
• Cuadrilátero: polígono con cuatro lados
• Pentágono: polígono con cinco lados
• Hexágono: polígono con seis lados
• Heptágono: polígono con siete lados
• Octógono: polígono con ocho lados
• Eneágono: polígono con nueve lados
• Decágono: polígono con diez lados
• Undecágono: polígono con once lados
• Dodecágono: polígono con doce lados

Por sus ángulos

Los podemos clasificar en cóncavos o convexos:

Un polígono será convexo, si todos sus ángulos son menores de 180°, por lo tanto, si determinamos dos puntos en su interior y los unimos con un segmento, éste siempre quedará en su interior.

Y será cóncavo, si al menos uno de sus ángulo mide más de 180°. Como muestra la figura, no todos los segmentos trazados entre dos puntos quedarán en su interior.

Como se calculan sus diagonales?

Las diagonales de un polígono son segmentos que unen dos vértices no consecutivos. 

El número de diagonales (D) de un polígono convexo (sea o no regular) viene determinado por el número de lados (N) que tiene el polígono. Su fórmula es: 

Ésto es así porque de cada vértice sale una diagonal a los demàs vértices, excepto a sí mismo y sus dos consecutives (de ahí el -3). Como una diagonal la trazamos entre dos vértices dos veces, una en cada sentido, el resultado del numerador se tiene que dividir por 2.

Ejemplo:

Un cuadrado tiene 4 lados. Se aplica la fórmula para comprobar el número de diagonales: 

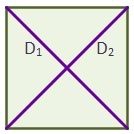
El cuadrado tiene dos diagonales. Si la longitud de los lados son conocidos, se puede calcular la longitud de las diagonales.

Como se calculan los ángulos de un polígono?

Son los determinados por dos lados consecutivos.

Suma de ángulos interiores de un polígono

Si n es el número de lados de un polígono: 

S= (n − 2) · 180°.

Suma de ángulos de un triángulo= (3 − 2) · 180° = 180º.

Suma de ángulos de un cuadrilátero= (4 − 2) · 180° = 360º.

Suma de ángulos de un pentágono= (5 − 2) · 180° = 540º.

Suma de ángulos de un hexágono= (5 − 2) · 180° = 720º.

Y así sucesivamente.